| TREEID | DIA (in) | HT (ft) | CRM biomass (lbs) | NSVB biomass (lbs) |
|---|---|---|---|---|
| 1 | 10.5 | 50 | 450.2 | 540.6 |
| 2 | 10.4 | 48 | 448.7 | 514.6 |
| 3 | 8.5 | 41 | 274.8 | 298.4 |
| 4 | 13.0 | 58 | 750.8 | 950.2 |
| 5 | 11.2 | 56 | 522.3 | 672.7 |
| 6 | 12.0 | 60 | 625.1 | 819.1 |
| 7 | 8.8 | 43 | 298.2 | 332.5 |
| 8 | 8.8 | 40 | 302.8 | 316.0 |
| 9 | 10.1 | 54 | 411.4 | 524.9 |
| 10 | 6.9 | 38 | 168.2 | 180.6 |
| 11 | 8.5 | 38 | 274.8 | 282.9 |
| 12 | 10.5 | 52 | 458.9 | 555.7 |
| 13 | 12.1 | 65 | 623.3 | 882.1 |
| 14 | 6.8 | 40 | 162.2 | 181.4 |
| 15 | 7.7 | 42 | 217.2 | 245.4 |
| 16 | 6.8 | 44 | 162.2 | 194.0 |
| 17 | 12.1 | 54 | 623.3 | 774.4 |
| 18 | 12.1 | 58 | 637.2 | 814.2 |
| 19 | 11.1 | 48 | 511.7 | 592.1 |
| 20 | 6.7 | 39 | 156.3 | 172.7 |

Anyone that’s taken an introductory statistics course has learned about hypothesis tests. Hypothesis tests are claims that we make about phenomena. Hypothesis tests allow us to make statements about whether the means or variances of data are equal to a unique value, or whether two groups of data are different.
Hypothesis tests are framed in terms of null and alternative hypotheses. The null hypothesis represents the hypothesis being tested. The null hypothesis is assumed to be true, but your data may provide evidence against it.
The alternative hypothesis represents the hypothesis that may be supported based on your data. Every hypothesis test results in one of two outcomes:
- The null hypothesis is rejected (i.e., the data support the alternative)
- The null hypothesis is accepted, or we fail to reject the null hypothesis (i.e., the data support the null).
Often more preferable over these “legacy” hypothesis tests, especially when evaluating models, is the use of equivalence tests. In hypothesis tests, the null states no difference between population means. Which from a model validation perspective indicates that the mean of the model outcomes is that same as the observations, or some other model being compared to.
In their 2005 paper, Robinson and Froese describe hypothesis tests as being problematic because “the burden of proof seems to be invested in the wrong side of the hypothesis.” Equivalence tests combat this problem, by “flipping the burden of proof” towards the model. Equivalence tests allow a dissimilarity region based on a specified threshold to generate disagreement between two values. In other words, the “null” hypothesis in an equivalence test assumes the two values are not similar, while the “alternative” indicates the two values are similar.
This post presents an application of equivalence tests comparing two estimates of tree biomass, with the supporting code in R.
Aspen biomass data
Twenty aspen trees from Minnesota, USA are used as example data. On these trees, diameter at breast height ranged from 6.7 to 13.0 inches. We seek to compare predictions of aboveground tree biomass from two different models. The first model makes predictions from the Component Ratio Method (CRM). A set of regional volume equations drive the CRM approach, which are then converted to tree biomass. The second model makes predictions from the National Scale Volume-Biomass Estimators (NSVB), a recently developed set of equations that replaced the CRM equations in estimates provided by the USDA Forest Service.
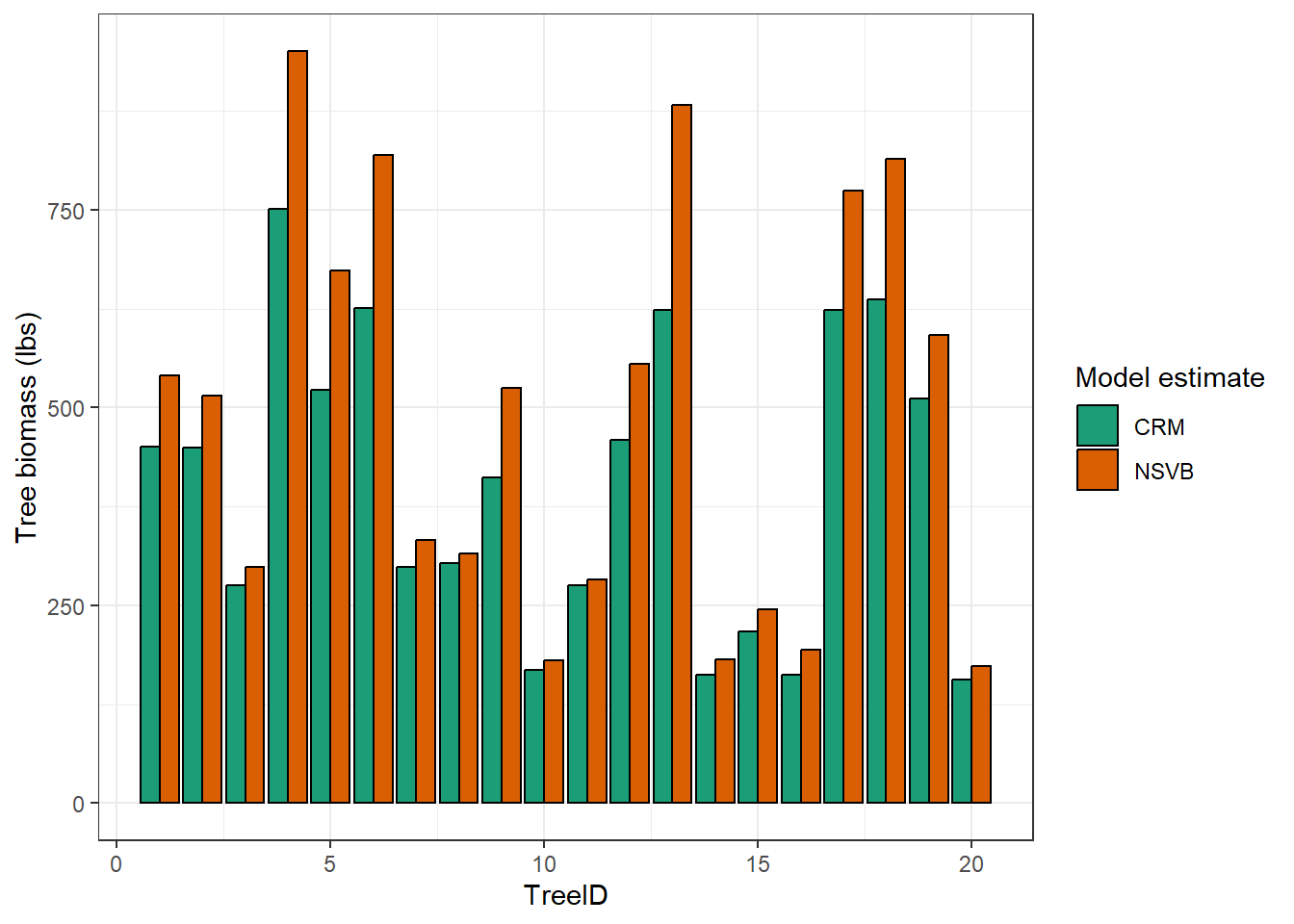
Here are the 20 aspen trees and their biomass predictions from the two models:
You’ll see below that the NSVB predictions for these aspen trees are greater than the CRM predictions for each tree. The finding that NSVB biomass predictions are greater than CRM ones was also described when these equations were expanded across the US:
t-test
First, let’s conduct a two-sample t-test using the t.test() function in R. We can specify a two-sided two-sample t-test at a level of significance of \(\alpha = 0.05\) that determines whether or not the two predictions of biomass are equal with the following hypotheses:
- The null hypothesis states that the mean of the CRM biomass is equal to the NSVB biomass.
- The alternative hypothesis states that the mean of the CRM biomass is not equal to the NSVB biomass.
We’ll assume the variances of both predictions are not equal using the var.equal = F statement:
t_test <- t.test(tree$AGB_NSVB, tree$AGB_CRM, var.equal = F)
print(t_test)
Welch Two Sample t-test
data: tree$AGB_NSVB and tree$AGB_CRM
t = 1.2281, df = 34.652, p-value = 0.2277
alternative hypothesis: true difference in means is not equal to 0
95 percent confidence interval:
-57.6855 234.1755
sample estimates:
mean of x mean of y
492.225 403.980 Note that the calculated t-statistic is 1.2281. The p-value of 0.2277 is greater than our level of significance of \(\alpha = 0.05\), hence, we have evidence to accept the null hypothesis and conclude that the CRM biomass predictions are equal to the NSVB biomass predictions.
Equivalence test
For conducting equivalence tests in R, the TOSTER package provides functions for computing two one-sided tests that can compared with the t-test. We’ll set the equivalence bounds for the test, or the regions where we would expect differences. This value can be subjective and is similar to the level of significance that is specified for a hypothesis test. However, it’s different because it is expressed in the units of the variable that we’re testing (i.e., in pounds of a tree in our example).
A common approach is to specify the magnitude of this region of similarity as a percentage of the standard deviation of the difference in the two values. This allows for some disagreement while still holding the model to strict accuracy standards. For example, we’ll assign the region of similarity to be +/- 25% of the standard deviation of the difference between CRM and NSVB biomass predictions, which is approximately 19 pounds:
tree <- tree |>
mutate(model_diff = AGB_NSVB - AGB_CRM)
sd_25 <- sd(tree$model_diff)*0.25
low_eqbound <- -sd_25
high_eqbound <- sd_25
low_eqbound; high_eqbound[1] -19.12677[1] 19.12677The tsum_TOST() function available in the TOTSER package can perform the two one-sided test of equivalence. We first specify the mean, standard deviation, and total number of observations for each variable (e.g., m1, sd1, and n1), then we specify the equivalence bounds:
library(TOSTER)
eq_test <- tsum_TOST(m1 = mean(tree$AGB_NSVB),
sd1 = sd(tree$AGB_NSVB),
n1 = length(tree$AGB_NSVB),
m2 = mean(tree$AGB_CRM),
sd2 = sd(tree$AGB_CRM),
n2 = length(tree$AGB_CRM),
low_eqbound = -sd_25,
high_eqbound = sd_25)
print(eq_test)
Welch Two Sample t-test
The equivalence test was non-significant, t(34.65) = 0.962, p = 8.29e-01
The null hypothesis test was non-significant, t(34.65) = 1.228, p = 2.28e-01
NHST: don't reject null significance hypothesis that the effect is equal to zero
TOST: don't reject null equivalence hypothesis
TOST Results
t df p.value
t-test 1.2281 34.65 0.228
TOST Lower 1.4942 34.65 0.072
TOST Upper 0.9619 34.65 0.829
Effect Sizes
Estimate SE C.I. Conf. Level
Raw 88.2450 71.8573 [-33.1963, 209.6863] 0.9
Hedges's g(av) 0.3799 0.3276 [-0.1371, 0.8914] 0.9
Note: SMD confidence intervals are an approximation. See vignette("SMD_calcs").You’ll first notice that the output provides results from a t-test, confirming the t-value of 1.2281 that we found above. The TOST results indicate a similar result to the t-test, that is we would not reject the null equivalence hypothesis and conclude the model results are similar. Note the output contains two p-values, one each for the lower and upper part of the test, along with the effect sizes.
I suspect the model predictions turn out to be equivalent here because of the relatively small difference we set in the equivalence bounds. After all, 19 pounds of biomass is not much of a difference in trees that are over 10 inches in diameter. You can continue to change the region of dissimilarity in the TOST function by modifying the low_eqbound and high_eqbound values. The smallest value in which the equivalence test result “flips” to indicate dissimilarity is termed the minimum detectable negligible difference. In this example, it happens if the equivalence bounds between CRM and NSVB predictions are set to approximately 210 pounds.
Instead of t-tests, give equivalence tests a try when evaluating models. In forestry we often have plenty of models available to us to compare predictions of volume and growth, either available in the literature or used in our own organization. Equivalence tests are an excellent approach the compare “old” models with a new and improved ones.
–
By Matt Russell. For more, subscribe to my monthly email newsletter to stay ahead on data and analytics trends in the forest products industry.